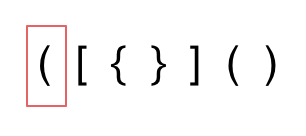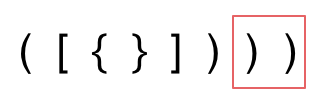Algorithm——Stack and Queue

发表于 2023-07-25 更新于 2023-07-28 分类于 Algorithm ， Stack and Queue 本文字数： 11k 阅读时长 ≈ 10 分钟

栈和队列

1. 理论基础

栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。

2. 用栈实现队列

232.请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例1

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

思路

使用栈来模式队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。

下面动画模拟以下队列的执行过程：

执行语句：
queue.push(1);
queue.push(2);
queue.pop(); 注意此时的输出栈的操作
queue.push(3);
queue.push(4);
queue.pop();
queue.pop();注意此时的输出栈的操作
queue.pop();
queue.empty();

232.stacktoq.gif 在push数据的时候，只要数据放进输入栈就好，但在pop的时候，操作就复杂一些，输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以了。

最后如何判断队列为空呢？如果进栈和出栈都为空的话，说明模拟的队列为空了。

在代码实现的时候，会发现pop() 和 peek()两个函数功能类似，代码实现上也是类似的，可以思考一下如何把代码抽象一下

代码

// 使用两个数组的栈方法（push, pop） 实现队列
/**
* Initialize your data structure here.
*/
var MyQueue = function() {
   this.stackIn = [];
   this.stackOut = [];
};

/**
* Push element x to the back of queue. 
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {
   this.stackIn.push(x);
};

/**
* Removes the element from in front of queue and returns that element.
* @return {number}
*/
MyQueue.prototype.pop = function() {
   const size = this.stackOut.length;
   if(size) {
       return this.stackOut.pop();
   }
   while(this.stackIn.length) {
       this.stackOut.push(this.stackIn.pop());
   }
   return this.stackOut.pop();
};

/**
* Get the front element.
* @return {number}
*/
MyQueue.prototype.peek = function() {
   const x = this.pop();
   this.stackOut.push(x);
   return x;
};

/**
* Returns whether the queue is empty.
* @return {boolean}
*/
MyQueue.prototype.empty = function() {
   return !this.stackIn.length && !this.stackOut.length
};

3. 用队列实现栈

225.请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例225

输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

思路

根据题意，要用两个队列来实现栈，首先我们知道，队列是先进先出，栈是后进先出。

知道了以上要点，我们两个队列的用处也就一目了然了。

一个队列为主队列，一个为辅助队列，当入栈操作时，我们先将主队列内容导入辅助队列，然后将入栈元素放入主队列队头位置，再将辅助队列内容，依次添加进主队列即可。

代码

// 使用两个队列实现
/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue1 = [];
    this.queue2 = [];
};

/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue1.push(x);
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    // 减少两个队列交换的次数， 只有当queue1为空时，交换两个队列
    if(!this.queue1.length) {
        [this.queue1, this.queue2] = [this.queue2, this.queue1];
    }
    while(this.queue1.length > 1) {
        this.queue2.push(this.queue1.shift());
    }
    return this.queue1.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue1.push(x);
    return x;
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue1.length && !this.queue2.length;
};

// 使用一个队列实现
/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue = [];
};

/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue.push(x);
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    let size = this.queue.length;
    while(size-- > 1) {
        this.queue.push(this.queue.shift());
    }
    return this.queue.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue.push(x);
    return x;
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue.length;
};

4. 有效的括号

20.给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号

1 2	输入：s = "()" 输出：true

1 2	输入：s = "()[]{}" 输出：true

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

思路

先来分析一下这里有三种不匹配的情况，

第一种情况，字符串里左方向的括号多余了，所以不匹配。
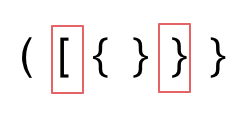
第二种情况，括号没有多余，但是括号的类型没有匹配上。
第三种情况，字符串里右方向的括号多余了，所以不匹配。

我们的代码只要覆盖了这三种不匹配的情况，就不会出问题，可以看出动手之前分析好题目的重要性。

动画如下：

20.有效括号

第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false

第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false

第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false

那么什么时候说明左括号和右括号全都匹配了呢，就是字符串遍历完之后，栈是空的，就说明全都匹配了。

代码

/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function(s) {
    const stack = [], 
        map = {
            "(":")",
            "{":"}",
            "[":"]"
        };
    for(const x of s) {
        if(x in map) {
            stack.push(x);
            continue;
        };
        if(map[stack.pop()] !== x) return false;
    }
    return !stack.length;
};

5. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例1

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

思路

本题也是用栈来解决的经典题目。

那么栈里应该放的是什么元素呢？

我们在删除相邻重复项的时候，其实就是要知道当前遍历的这个元素，我们在前一位是不是遍历过一样数值的元素，那么如何记录前面遍历过的元素呢？

所以就是用栈来存放，那么栈的目的，就是存放遍历过的元素，当遍历当前的这个元素的时候，去栈里看一下我们是不是遍历过相同数值的相邻元素。

然后再去做对应的消除操作。如动画所示：

1047.删除字符串中的所有相邻重复项

从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以再对字符串进行反转一下，就得到了最终的结果。

代码

/**
 * @param {string} s
 * @return {string}
 */
var removeDuplicates = function(s) {
const result = []
    for(const i of s){
        if(i === result[result.length-1]){
            result.pop()
        }else{
            result.push(i)
        }
    }
    return result.join('')
};

6. 逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 ‘+’、’-‘、’*’ 和 ‘/‘ 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是向零截断。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位整数表示。

1
2
3

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

1
2
3

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

思路

逆波兰表达式：是一种后缀表达式，所谓后缀就是指运算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。

该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。

本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这岂不就是一个相邻字符串消除的过程，和删除字符串中的所有相邻重复项中的对对碰游戏是不是就非常像了。

如动画所示： 150.逆波兰表达式求值

代码

/**
 * @param {string[]} tokens
 * @return {number}
 */
var evalRPN = function (tokens) {
    const stack = [];
    for (const token of tokens) {
        if (isNaN(Number(token))) { // 非数字
            const n2 = stack.pop(); // 出栈两个数字
            const n1 = stack.pop();
            switch (token) { // 判断运算符类型，算出新数入栈
                case "+":
                    stack.push(n1 + n2);
                    break;
                case "-":
                    stack.push(n1 - n2);
                    break;
                case "*":
                    stack.push(n1 * n2);
                    break;
                case "/":
                    stack.push(n1 / n2 | 0);
                    break;
            }
        } else { // 数字
            stack.push(Number(token));
        }
    }
    return stack[0]; // 因没有遇到运算符而待在栈中的结果
};

7. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例1
示例2

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

1 2	输入：nums = [1], k = 1 输出：[1]

思路

维护单调递减队列，当进入滑动窗口的元素大于等于队尾的元素时不断从队尾出队，直到进入滑动窗口的元素小于队尾的元素，才可以入队，以保证单调递减的性质，当队头元素已经在滑动窗口外了，移除对头元素，当i大于等于k-1的时候，单调递减队头就是滑动窗口的最大值

代码

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function (nums, k) {
    const q = [];//单递减的双端队列
    const ans = [];//最后的返回结果
    for (let i = 0; i < nums.length; i++) {//循环nums
        //当进入滑动窗口的元素大于等于队尾的元素时 不断从队尾出队，
        //直到进入滑动窗口的元素小于队尾的元素，以保证单调递减的性质
        while (q.length && nums[i] >= nums[q[q.length - 1]]) {
            q.pop();
        }
        q.push(i);//元素的索引入队
        while (q[0] <= i - k) {//队头元素已经在滑动窗口外了，移除对头元素
            q.shift();
        }
        //当i大于等于k-1的时候，单调递减队头就是滑动窗口的最大值
        if (i >= k - 1) ans.push(nums[q[0]]);
    }
    return ans;
};

8. 前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例1
示例2

1 2	输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2]

1 2	输入: nums = [1], k = 1 输出: [1]

思路

寻找前k个最大元素流程如图所示：（图中的频率只有三个，所以正好构成一个大小为3的小顶堆，如果频率更多一些，则用这个小顶堆进行扫描）

347.前K个高频元素

代码

let topKFrequent = function(nums, k) {
    let map = new Map(), arr = [...new Set(nums)]
    nums.map((num) => {
        if(map.has(num)) map.set(num, map.get(num)+1)
        else map.set(num, 1)
    })

    return arr.sort((a, b) => map.get(b) - map.get(a)).slice(0, k);
};

let topKFrequent = function(nums, k) {
    let map = new Map(), heap = [,]
    nums.map((num) => {
        if(map.has(num)) map.set(num, map.get(num)+1)
        else map.set(num, 1)
    })

    // 如果元素数量小于等于 k
    if(map.size <= k) {
        return [...map.keys()]
    }

    // 如果元素数量大于 k，遍历map，构建小顶堆
    let i = 0
    map.forEach((value, key) => {
        if(i < k) {
            // 取前k个建堆, 插入堆
            heap.push(key)
            // 原地建立前 k 堆
            if(i === k-1) buildHeap(heap, map, k)
        } else if(map.get(heap[1]) < value) {
            // 替换并堆化
            heap[1] = key
            // 自上而下式堆化第一个元素
            heapify(heap, map, k, 1)
        }
        i++
    })
    // 删除heap中第一个元素
    heap.shift()
    return heap
};

// 原地建堆，从后往前，自上而下式建小顶堆
let buildHeap = (heap, map, k) => {
    if(k === 1) return
    // 从最后一个非叶子节点开始，自上而下式堆化
    for(let i = Math.floor(k/2); i>=1 ; i--) {
        heapify(heap, map, k, i)
    }
}

// 堆化
let heapify = (heap, map, k, i) => {
    // 自上而下式堆化
    while(true) {
        let minIndex = i
        if(2*i <= k && map.get(heap[2*i]) < map.get(heap[i])) {
            minIndex = 2*i
        }
        if(2*i+1 <= k && map.get(heap[2*i+1]) < map.get(heap[minIndex])) {
            minIndex = 2*i+1
        }
        if(minIndex !== i) {
            swap(heap, i, minIndex)
            i = minIndex
        } else {
            break
        }
    }
}

// 交换
let swap = (arr, i , j) => {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}