Algorithm——Array

发表于 更新于 分类于 ， 本文字数： 19k 阅读时长 ≈ 17 分钟

数组

1.数组理论基础

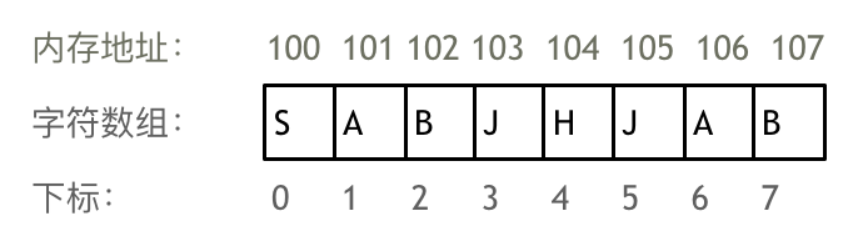
数组是存放在连续内存空间上的相同类型数据的集合

数组可以通过下标索引的方式获取下标下对应的数据

注意

  • 数组下标都是从0开始的

  • 数组内存空间的地址是连续的

  • 数组的元素是不能删的，只能覆盖

2.！二分查找

704.给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4
1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1

提示：

  • 可以假设nums中的所有元素是不重复的

  • n将在[1,10000]之间

  • nums的每个元素都将在[-9999,9999]之间

思路

  • 数组为有序数组

  • 数组中无重复元素

    • 存在重复元素，使用二分查找法返回的元素下标可能不是唯一的

满足上述两点可考虑二分法

二分法的区间定义就是不变量

  • 在二分查找过程中，保持不变量，即在while寻找中每一次边界处理都要坚持根据区间的定义来操作

二分法区间定义

  • 左闭右闭[left,right]

    • while(left<=right)要使用<=，因为left == right是有意义的

    • if [ num[middle] > target ) right要赋值为 middle - 1 ；因为当前nums[middle]一定不是target，那么下面查找的左区间结束下标位置就是middle - 1

    • 时间复杂度：O(log n)

    • 空间复杂度：O(1)

  • 左闭右开[left,right)

    • while(left < right),因为left == right在区间中是没有意义的

    • if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

代码

左闭右闭区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    let mid, left = 0, right = nums.length - 1;
    // 当left=right时，由于nums[right]在查找范围内，所以要包括此情况
    while (left <= right) {
        // 位运算 + 防止大数溢出
        mid = left + ((right - left) >> 1);
        // 如果中间数大于目标值，要把中间数排除查找范围，所以右边界更新为mid-1；如果右边界更新为mid，那中间数还在下次查找范围内
        if (nums[mid] > target) {
            right = mid - 1;  // 去左面闭区间寻找
        } else if (nums[mid] < target) {
            left = mid + 1;   // 去右面闭区间寻找
        } else {
            return mid;
        }

 }
    return -1;
}

左闭右开区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    // right是数组最后一个数的下标+1，nums[right]不在查找范围内，是左闭右开区间
    let mid, left = 0, right = nums.length;    
    // 当left=right时，由于nums[right]不在查找范围，所以不必包括此情况
    while (left < right) {
        // 位运算 + 防止大数溢出
        mid = left + ((right - left) >> 1);
        // 如果中间值大于目标值，中间值不应在下次查找的范围内，但中间值的前一个值应在；
        // 由于right本来就不在查找范围内，所以将右边界更新为中间值，如果更新右边界为mid-1则将中间值的前一个值也踢出了下次寻找范围
        if (nums[mid] > target) {
            right = mid;  // 去左区间寻找
        } else if (nums[mid] < target) {
            left = mid + 1;   // 去右区间寻找
        } else {
            return mid;
        }
    }
    return -1;
};

相关题目

-35.搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

1
2
输入: nums = [1,3,5,6], target = 5
输出: 2
1
2
输入: nums = [1,3,5,6], target = 2
输出: 1
1
2
输入: nums = [1,3,5,6], target = 7
输出: 4

提示

  • 1 <= nums.length <= 10^4

  • -10^4 <= nums[i] <= 10^4

  • nums 为 无重复元素 的 升序 排列数组

  • -10^4 <= target <= 10^4

思路

存在以下四种情况

  • 目标值在数组所有元素之前
  • 目标值等于数组中某一个元素
  • 目标值插入数组中的位置
  • 目标值在数组所有元素之后
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var searchInsert = function(nums, target) {
    let left = 0;
    let mid = 0;
    let right = nums.length - 1;
    while(left <= right){
        mid = left + ((right - left) >> 1);
        if(nums[mid] < target){
            left = mid + 1;
        }else if(nums[mid] > target){
            right = mid - 1;
        }else{
            return mid;
        }
    }
    return left;
    /*return right +1*/
};

-34.在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

1
2
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]]
1
2
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]
1
2
输入：nums = [], target = 0
输出：[-1,-1]

提示

  • 0 <= nums.length <= 10^5

  • -10^9 <= nums[i] <= 10^9

  • nums 是一个非递减数组

  • -10^9 <= target <= 10^9

思路

寻找target在数组里的左右边界，有如下三种情况：

  • 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
  • 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
  • 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
var searchRange = function(nums, target) {
    const getLeftBorder = (nums, target) => {
        let left = 0, right = nums.length - 1;
        let leftBorder = -2;// 记录一下leftBorder没有被赋值的情况
        while(left <= right){
            let middle = left + ((right - left) >> 1);
            if(nums[middle] >= target){ // 寻找左边界，nums[middle] == target的时候更新right
                right = middle - 1;
                leftBorder = right;
            } else {
                left = middle + 1;
            }
        }
        return leftBorder;
    }

    const getRightBorder = (nums, target) => {
        let left = 0, right = nums.length - 1;
        let rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
        while (left <= right) {
            let middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle - 1;
            } else { // 寻找右边界，nums[middle] == target的时候更新left
                left = middle + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }

    let leftBorder = getLeftBorder(nums, target);
    let rightBorder = getRightBorder(nums, target);
    // 情况一
    if(leftBorder === -2 || rightBorder === -2) return [-1,-1];
    // 情况三
    if (rightBorder - leftBorder > 1) return [leftBorder + 1, rightBorder - 1];
    // 情况二
    return [-1, -1];
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var searchRange = function(nums, target) {
    let left = 0
    let right = nums.length - 1;

    while(left <= right) {
        let mid = (left + right) >> 1

        if (nums[mid] === target) {
            let tempLeft = tempRight = mid ;
            while(nums[tempLeft - 1] === target) tempLeft--;
            while(nums[tempRight + 1] === target) tempRight++;
            return [tempLeft, tempRight]
        } else if (nums[mid] > target) {
            right = mid - 1
        } else {
            left = mid + 1
        }
    }
    return [-1, -1]
};

-69.x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意： 不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

1
2
输入：x = 4
输出：2
1
2
3
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去

提示：

  • 0 <= x <= 2^31 - 1
思路

  • 整数x的平方根一定小于或等于x

  • 除0之外的所有整数的平方根都大于或等于1

  • 整数x的平方根一定是在1到x的范围内，取这个范围内的中间数字mid，并判断mid的平方是否小于或等于x

    • 如果mid的平方小于x,那么接着判断(mid+1)的平方是否大于x，如果(mid+1)的平方大于x，那么mid就是x的平方根

    • 如果mid的平方小于x并且(mid+1)的平方小于x，那么x的平方根比mid大，接下来搜索从mid+1到x的范围

    • 如果mid的平方大于x，则x的平方根小于mid，接下来搜索1到mid-1的范围

    • 然后在相应的范围内重复这个过程，总是取出位于范围中间的mid

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @param {number} x
 * @return {number}
 */
var mySqrt = function (x) {
  // 整数x的平方根一定是在1到x的范围内
  let left = 1;
  let right = x;
  while (left <= right) {
    // 中间值  下面这样写是防止溢出
    let mid = left + ((right - left) >> 1);
    // 判断mid的平方是否小于或等于x，如果mid的平方小于x
    if (mid <= x / mid) {
      // 判断(mid+1)的平方是否大于x，如果(mid+1)的平方大于x，那么mid就是x的平方根
      if (mid + 1 > x / (mid + 1)) {
        return mid;
      }
      // 如果mid的平方小于x并且(mid+1)的平方小于x，那么x的平方根比mid大，接下来搜索从mid+1到x的范围
      left = mid + 1;
    } else {
      // 如果mid的平方大于x，则x的平方根小于mid，接下来搜索1到mid-1的范围
      right = mid - 1;
    }
  }
  // 如果输入参数是0，left等于1而right等于0，就直接返回0
  return 0;
};

-367.有效的完全平方数

给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如  sqrt 。

1
2
3
输入：num = 16
输出：true
解释：返回 true ，因为 4 * 4 = 16 且 4 是一个整数。
1
2
3
输入：num = 14
输出：false
解释：返回 false ，因为 3.742 * 3.742 = 14 但 3.742 不是一个整数
思路

  • num 是正整数，若正整数 x 满足x*x = num,则x一定满足1<= x <= num;

  • 1 和 num 作为二分查找搜索区间的初始边界。

  • 时间复杂度：O(log n),n为正整数num的最大值

  • 空间复杂度：O(1)

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @param {number} num
 * @return {boolean}
 */
var isPerfectSquare = function(num) {
    let left = 0, right = num;
    while (left <= right) {
        const mid = Math.floor((right - left) / 2) + left;
        const square = mid * mid;
        if (square < num) {
            left = mid + 1;
        } else if (square > num) {
            right = mid - 1;
        } else {
            return true;
        }
    }
    return false;
};

3.移除元素

27.给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

1
2
3
4
5
6
7
8
// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}
1
2
3
输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。
1
2
3
输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

思路

要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖

！双指针法

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

  • 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组

  • 慢指针：指向更新 新数组下标的位置

  • 时间复杂度：O(n)

  • 空间复杂度：O(1)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * @param {number[]} nums
 * @param {number} val
 * @return {number}
 */
var removeElement = function(nums, val) {
    let k = 0;
    for(let i = 0;i < nums.length;i++){
        if(nums[i] != val){
            nums[k] = nums[i];
            k++;
        }
    }
    return k;
};

相关题目

-26.删除排序数组中的重复项

给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 **只出现一次 **，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

  • 更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。

  • 返回 k 。

判题标准:

系统会用下面的代码来测试你的题解:

1
2
3
4
5
6
7
8
9
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}
1
2
3
输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
1
2
3
输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
思路

  • 数组nums有序的，只能在原地修改nums数组，不能创建新的数组空间来存储删除重复出现的元素后的结果。

  • 需要一边遍历数组查找相同元素，一边在对比发现不同元素时修改数组元素，

  • 考虑双指针法的快慢指针

    • 定义slow和fast作为指针

    • 初始化时指针slow指向数组的起始位置（nums[0]）

    • 随着指针fast不断向后移动，将指针fast指向的元素与指针slow指向的元素进行比较

      • 如果nums[fast] ≠ nums[slow]，那么nums[slow + 1] = nums[fast]

      • 如果nums[fast] = nums[slow]，那么指针fast继续向后查找

  • 时间复杂度：O(n)

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {number[]} nums
 * @return {number}
 */
var removeDuplicates = function(nums) {
    if(nums.length == 0){return 0;}
    let slow = 0, fast = 1;
    while(fast < nums.length){
        if(nums[fast] != nums[slow]){
            slow = slow + 1;
            nums[slow] = nums[fast];
        }
        fast = fast + 1;
    }
    return slow + 1;
};

-283.移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

1
2
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
1
2
输入: nums = [0]
输出: [0]
思路

相当于对整个数组移除元素0，然后slowIndex之后都是移除元素0的冗余元素，把这些元素都赋值为0就可以了。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {number[]} nums
 * @return {void} Do not return anything, modify nums in-place instead.
 */
var moveZeroes = function(nums) {
        let slow = 0;
        for (let fast = 0; fast < nums.length; fast++) {
            if (nums[fast] != 0) {
                nums[slow++] = nums[fast];
            }
        }
        // 后面的元素全变成 0
        for (let j = slow; j < nums.length; j++) {
            nums[j] = 0;
        }
};

-844.比较含退格的字符串

给定 s 和 t 两个字符串，当它们分别被输入到空白的文本编辑器后，如果两者相等，返回 true 。# 代表退格字符。

注意 :如果对空文本输入退格字符，文本继续为空。

1
2
3
输入：s = "ab#c", t = "ad#c"
输出：true
解释：s 和 t 都会变成 "ac"
1
2
3
输入：s = "ab##", t = "c#d#"
输出：true
解释：s 和 t 都会变成 ""。
1
2
3
输入：s = "a#c", t = "b"
输出：false
解释：s 会变成 "c"，但 t 仍然是 "b"。
思路

  • 准备指针i``j分别指向S``T的末位字符，再准备变量skipS,skipT来存放S,T字符串中的#数量

  • 从后向前遍历S，遇到以下情况

    • 若当前字符为#，则skipS自增1

    • 若当前字符不是#，且skipS 不为0，则skipS自减1

    • 若当前字符不是#，且skipS为0，则代表当前字符不会被消除，我们可以用来和 T 中的当前字符作比较。

  • 若对比过程中S,T当前字符不匹配，则遍历结束，返回false

  • 若遍历结束，且一一匹配，则返回true

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * @param {string} s
 * @param {string} t
 * @return {boolean}
 */
var backspaceCompare = function(s, t) {
    let i = s.length - 1,
        j = t.length - 1,
        skipS = 0,
        skipT = 0;
    // 大循环
    while(i >= 0 || j >= 0){
        // S 循环
        while(i >= 0){
            if(s[i] === '#'){
                skipS++;
                i--;
            }else if(skipS > 0){
                skipS--;
                i--;
            }else break;
        }
        // T 循环
        while(j >= 0){
            if(t[j] === '#'){
                skipT++;
                j--;
            }else if(skipT > 0){
                skipT--;
                j--;
            }else break;
        }
        if(s[i] !== t[j]) return false;
        i--;
        j--;
    }
    return true;
};

-977.有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序

思路

  • 数组其实是有序的， 只不过负数平方之后可能成为最大数了。

  • 那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

  • 此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

  • 定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置

  • 如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]

  • 如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]

  • 时间复杂度为O(n)

1
2
3
4
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
1
2
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number[]} nums
 * @return {number[]}
 */
var sortedSquares = function(nums) {
    let res = []
    for (let i = 0, j = nums.length - 1; i <= j;) {
      const left = Math.abs(nums[i])
      const right = Math.abs(nums[j])
      if (right > left) {
        // push element to the front of the array
        res.unshift(right * right)
        j--
      } else {
        res.unshift(left * left)
        i++
      }
    }
    return res
};

4.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 

1
2
3
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
1
2
输入：target = 4, nums = [1,4,4]
输出：1
1
2
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

思路

窗口是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

！滑动窗口

就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果

只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置

确定如下三点：

  • 窗口内是什么？
  • 如何移动窗口的起始位置？
  • 如何移动窗口的结束位置？

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @param {number} target
 * @param {number[]} nums
 * @return {number}
 */
var minSubArrayLen = function(target, nums) {
    let start, end
    start = end = 0
    let sum = 0
    let len = nums.length
    let ans = Infinity

    while(end < len){
        sum += nums[end];
        while (sum >= target) {
            ans = Math.min(ans, end - start + 1);
            sum -= nums[start];
            start++;
        }
        end++;
    }
    return ans === Infinity ? 0 : ans
};

相关题目

-904.水果成篮

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

  • 你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。

  • 你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。

  • 一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

1
2
3
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。
1
2
3
4
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。
1
2
3
4
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。
1
2
3
输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。
思路

用滑动窗口遍历fruits，当有新种类的水果进入窗口时

  • 如果窗口中只有一种水果，将这种水果加入arr数组

  • 如果有两种水果，更新窗口的左边界，更新arr中水果的种类

  • 如果进来了一种新的类型的水果 更新前一种水果的位置

  • 更新滑动窗口的最大值

  • 时间复杂度O(n)

  • 空间复杂度O(1)。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @param {number[]} fruits
 * @return {number}
 */
var totalFruit = function(fruits) {

    let l = 0;//起始指针
    let maxLen = 0;//窗口的最大长度 其中最多包涵两种水果
    let n = 0//前一类水果的结束位置
    let arr = [fruits[l]]//水果的种类数组

    for(let r = 0; r < fruits.length; r++){//窗口的右指针不断前进
        if(!arr.includes(fruits[r])){//如果窗口中不包含 进窗口的水果
            if(arr.length <= 1){//如果只有一种水果
                arr[1] = fruits[r]//将这种水果加入arr数组
            }else{//如果有两种水果
                l = n//更新窗口的左边界
                arr[0] = fruits[r-1]//更新arr中水果的种类
                arr[1] = fruits[r]
            }
        }

        if(fruits[r] !== fruits[n]){//如果进来了一种新的类型的水果 更新前一种水果的位置
            n = r
        }

        maxLen = Math.max(maxLen,r-l+1)//更新滑动窗口的最大值
    }
    return maxLen
};

-76.最小覆盖字串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。
1
2
3
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
1
2
3
输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。
1
2
3
4
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。
思路

使用两个指针一个left，一个right，分别表示窗口的左边界和右边界。

  • 当窗口内的所有字符不能覆盖t的时候，要扩大窗口，也就是right往右移。

  • 当窗口内的所有字符可以覆盖t的时候，记录窗口的起始位置以及窗口的长度，然后缩小窗口（因为这里求的是能覆盖的最小子串），left往右移。如果缩小的窗口还能覆盖t，保存长度最小的窗口即可。

  • 重复上面的操作，直到窗口的右边不能再移动为止。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
var minWindow = function(s, t) {
  let minLen = s.length + 1;
  let start = s.length;     // 结果子串的起始位置
  let map = {};             // 存储目标字符和对应的缺失个数
  let missingType = 0;      // 当前缺失的字符种类数
  for (const c of t) {      // t为baac的话，map为{a:2,b:1,c:1}
    if (!map[c]) {
      missingType++;        // 需要找齐的种类数 +1
      map[c] = 1;
    } else {
      map[c]++;
    }
  }
  let l = 0, r = 0;                // 左右指针
  for (; r < s.length; r++) {      // 主旋律扩张窗口，超出s串就结束
    let rightChar = s[r];          // 获取right指向的新字符
    if (map[rightChar] !== undefined) map[rightChar]--; // 是目标字符，它的缺失个数-1
    if (map[rightChar] == 0) missingType--;   // 它的缺失个数新变为0，缺失的种类数就-1
    while (missingType == 0) {                // 当前窗口包含所有字符的前提下，尽量收缩窗口
      if (r - l + 1 < minLen) {    // 窗口宽度如果比minLen小，就更新minLen
        minLen = r - l + 1;
        start = l;                 // 更新最小窗口的起点
      }
      let leftChar = s[l];          // 左指针要右移，左指针指向的字符要被丢弃
      if (map[leftChar] !== undefined) map[leftChar]++; // 被舍弃的是目标字符，缺失个数+1
      if (map[leftChar] > 0) missingType++;      // 如果缺失个数新变为>0，缺失的种类+1
      l++;                          // 左指针要右移 收缩窗口
    }
  }
  if (start == s.length) return "";
  return s.substring(start, start + minLen); // 根据起点和minLen截取子串
};

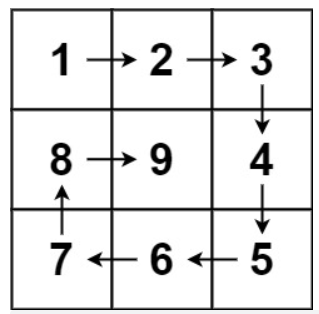
5. 螺旋矩阵II

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix

1
2
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
1
2
输入：n = 1
输出：[[1]]

思路

坚持循环不变量原则。

模拟顺时针画矩阵的过程:

  • 填充上行从左到右
  • 填充右列从上到下
  • 填充下行从右到左
  • 填充左列从下到上

这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function(n) {
  let startX = startY = 0;   // 起始位置
    let loop = Math.floor(n/2);   // 旋转圈数
    let mid = Math.floor(n/2);    // 中间位置
    let offset = 1;    // 控制每一层填充元素个数
    let count = 1;     // 更新填充数字
    let res = new Array(n).fill(0).map(() => new Array(n).fill(0));

    while (loop--) {
        let row = startX, col = startY;
        // 上行从左到右（左闭右开）
        for (; col < startY + n - offset; col++) {
            res[row][col] = count++;
        }
        // 右列从上到下（左闭右开）
        for (; row < startX + n - offset; row++) {
            res[row][col] = count++;
        }
        // 下行从右到左（左闭右开）
        for (; col > startY; col--) {
            res[row][col] = count++;
        }
        // 左列做下到上（左闭右开）
        for (; row > startX; row--) {
            res[row][col] = count++;
        }

        // 更新起始位置
        startX++;
        startY++;

        // 更新offset
        offset += 2;
    }
    // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
    if (n % 2 === 1) {
        res[mid][mid] = count;
    }
    return res;
}; 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function(n) {
        let l = 0, r = n - 1, t = 0, b = n - 1;
        let num = 1, tar = n * n;
        let mat = new Array(n).fill(0).map(() => new Array(n).fill(0));
        while(num <= tar){
            for(let i = l; i <= r; i++) mat[t][i] = num++; // left to right.
            t++;
            for(let i = t; i <= b; i++) mat[i][r] = num++; // top to bottom.
            r--;
            for(let i = r; i >= l; i--) mat[b][i] = num++; // right to left.
            b--;
            for(let i = b; i >= t; i--) mat[i][l] = num++; // bottom to top.
            l++;
        }
        return mat;
    };

相关题目

-54.螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素

提示：

  • m == matrix.length

  • n == matrix[i].length

  • 1 <= m, n <= 10

  • -100 <= matrix[i][j] <= 100

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]]
1
2
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
思路

  • 如果一条边从头遍历到底，则下一条边遍历的起点随之变化

  • 选择不遍历到底，可以减小横向、竖向遍历之间的影响

  • 一轮迭代结束时，4条边的两端同时收窄 1

  • 一轮迭代所做的事情变得很清晰：遍历一个“圈”，遍历的范围收缩为内圈

  • 一层层向里处理，按顺时针依次遍历：上、右、下、左。

  • 不再形成“环”了，就会剩下：一行或一列，然后单独判断

四个边界

  • 上边界 top : 0

  • 下边界 bottom : matrix.length - 1

  • 左边界 left : 0

  • 右边界 right : matrix[0].length - 1

矩阵不一定是方阵

  • top < bottom && left < right 是循环的条件

  • 无法构成“环”了，就退出循环，退出时可能是这 3 种情况之一：

    • top == bottom && left < right —— 剩一行

    • top < bottom && left == right —— 剩一列

    • top == bottom && left == right —— 剩一项（也算 一行/列）

    • 处理剩下的单行或单列

      • 因为是按顺时针推入结果数组的，所以

      • 剩下的一行，从左至右 依次推入结果数组

      • 剩下的一列，从上至下 依次推入结果数

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function(matrix) {
    if (matrix.length === 0) return []
    const res = []
    let top = 0, bottom = matrix.length - 1, left = 0, right = matrix[0].length - 1
    while (top < bottom && left < right) {
        for (let i = left; i < right; i++) res.push(matrix[top][i])   // 上层
        for (let i = top; i < bottom; i++) res.push(matrix[i][right]) // 右层
        for (let i = right; i > left; i--) res.push(matrix[bottom][i])// 下层
        for (let i = bottom; i > top; i--) res.push(matrix[i][left])  // 左层
        right--
        top++
        bottom--
        left++  // 四个边界同时收缩，进入内层
    }
    if (top === bottom) // 剩下一行，从左到右依次添加
        for (let i = left; i <= right; i++) res.push(matrix[top][i])
    else if (left === right) // 剩下一列，从上到下依次添加
        for (let i = top; i <= bottom; i++) res.push(matrix[i][left])
    return res
};

内容来源链接：力扣